Measuring Halo Effects in Media Mix Modeling

In MMM, spillover (also known as halo effects) represents the indirect impact of marketing activities across different channels, products, or geographies. Unlike direct effects, through which the impact of marketing spending is immediately visible on the targeted channel or product, halo effects are more subtle and complex. They can amplify (or sometimes diminish) the effectiveness of marketing campaigns in ways that are not immediately apparent.

Understanding Halo Effects

A halo effect occurs when marketing activities on a campaign or channel impact something else downstream. Halo effects can arise in multiple scenarios. One example could be that promoting product A inadvertently drives sales to product B. Another would be that spending on a top-of-funnel campaign drives people to other campaigns at the bottom of the funnel. These halo effects can also occur across channels such that spending on a TV ad could push people to search on Google. As I have discussed before, it is helpful to visualize the interconnectivity of our marketing activity to better understand how to formulate our problem.

Figure 1. Bottom-of-Funnel Halo Effects Caused by Top-of-Funnel Activity

As you can see from Figure 1, top-of-funnel (ToFu) activity impacts bottom-of-funnel (BoFu) activity and directly affects revenue. In marketing, this could be the case if we have a marketing campaign in the form of a TV ad that drives someone to search on Google but also drives someone else to go directly to our store and make a purchase.

Measuring and Modeling Halo Effects

Measuring and modeling halo effects in Media Mix Modeling presents a complex challenge, primarily due to the intricate and often subtle ways in which different marketing channels and efforts influence each other. Luckily, there is no shortage of tools we can use to attempt to measure these complicated effects. I will review econometrics, time series, and structural equation models, but there are many other techniques that we could utilize.

Econometric Models with Time Lags and Interaction Terms

Time-lagged models allow us to utilize the foundational principles of multiple linear regression but extend the concepts. This enables us to capture the nuanced, delayed effects that marketing activities can have over time. We are curious about how to measure halo effects, and we can add a unique set of terms to these models (called interaction terms) to attempt to measure them.

These terms, crafted by multiplying two or more variables, can measure the synergistic or antagonistic forces between marketing interventions. For instance, we can measure the interplay between top-of-funnel initiatives and bottom-of-funnel tactics. This interaction term directly measures their combined impact, indicating whether there is a halo effect. The interaction term between BoFu and ToFu measures whether sales were elevated beyond what we’d anticipate from each tactic in isolation.

These models and their extensions are the most common models in MMM and in measuring halo effects. Using an interaction term is easily interpretable and common in economic analysis. Examples of this type of model in practice are Naik and Kay Peters (2009), Norris et al. (2012), and Dinner et al. (2014).

Imagine extending our discussion from Figure 1 to consider the immediate impact of ToFu activities on BoFu outcomes and how these effects unfold over subsequent periods. We can formulate the problem as follows:

$Y_t = \beta_0 + \beta_1 ToFu_{t-l} + \beta_2 BoFu_{t-l} + \beta_3 (ToFu_{t-l} \times BoFu_{t-l}) + \epsilon_t$

Notice the $t - 1$ subscript in the above equation; this shows we are considering the last period’s value when measuring the current period. In this case, we are assuming a time lag of 1 period. We can select and combine multiple time lags to measure how an investment in ToFu might boost BoFu metrics in the current period and how it continues to exert influence over the following periods. Also, notice the $\beta_3 (ToFu_{t-l} \times BoFu_{t-l})$ term; this is attempting to measure the incremental impact of ToFu and BoFu together, which is our halo effect.

The Pros and Cons of Time-Lagged Models

The benefit of these models is that integrating time lags is relatively straightforward. Multiple open-source libraries exist that offer robust support for such models. These models are often easily interpretable, and extracting impacts is trivial, making them a great starting point.

These models have downsides, one of which is the linear assumptions they make. The real-world interplay of marketing variables is often far from linear, especially when considering temporal dynamics. Additionally, pinpointing the optimal lag length is complex, and selecting the wrong values can hamstring the resulting model.

We can overcome some of these issues through more advanced techniques. For example, we can utilize non-linear terms in our analysis (splines, polynomials, or more interaction terms) to help model non-linear relationships. We can also apply logarithmic transformations to the data to help linearize the relationships we seek to measure.

Lastly, Generalized Additive Models (GAMs) are natural extensions of traditional econometric models. While traditional econometric models impose a fixed linear form on the relationship between predictors and the outcome variable, GAMs offer a more flexible approach by allowing the form of the relationship to be determined by the data. To help select the optimal lag period(s), we can utilize cross-validation to choose the number of lags that cause the best performance. We can also use the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) to select the optimal number of lags. AIC and BIC measure how different values balance model fit and complexity.

Time-Series Analysis with Intervention Modeling

Another tool we have up our sleeve is time-series-based methods. Time-series modeling focuses on understanding data points collected over time and using the temporal structure of the data to make forecasts. In MMM, we can use time-series models while accounting for trends, seasonality, and autocorrelation in the data to model our marketing activities. We can extend the traditional time-series model by incorporating external interventions, such as marketing campaigns, to assess their impact and how they relate to other campaigns.

Since marketing data typically comes to us in a temporal format, we can model our marketing as interventions, which allows us to witness how specific marketing campaigns or changes in strategy play out over time. Analysts can quantify their immediate and delayed effects on sales or other KPIs by treating these events as interventions in a time-series model.

Standard time-series techniques (ARIMA, ARMA, etc.) are relatively rare in halo effect measurement. However, a standard extension to these models, vector autoregression (VAR), is frequently seen in research. An example of this is Dekimpe & Hanssens (2004).

One way to model this data is to create a baseline time-series model (like ARIMA), which seeks to model the series without any interventions. This model accounts for the time series autocorrelation, seasonality, and trend.

$Y_t = c + \phi_1 Y_{t-1} + \dots + \phi_p Y_{t-p} + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q} + \varepsilon_t$

In this equation:

$Y_t$ is the time series at time $t$ .
$c$ is a constant.
$\phi_1, \dots, \phi_p$ are the coefficients for the autoregressive terms.
$\theta_1, \dots, \theta_q$ are the coefficients for the moving average terms.
$\varepsilon_t$ is the error term at time $t$ .

Remember that in this context, $Y_t$ is the outcome variable that you suspect is influenced by the halo effect. Using our earlier example from Figure 1, this would be activity on our BoFu channel.

Once this model is built and validated, we can introduce an intervention variable representing our marketing intervention. (Again, our intervention is activity on our ToFu channel.)This variable is often binary and often takes two forms:

Constant effect: 0s before the intervention and 1s after.
Pulse effect: A single 1 at the time of intervention and 0s elsewhere.

$Y_t = c + \phi_1 Y_{t-1} + \dots + \phi_p Y_{t-p} + \theta_1 \varepsilon_{t-1} + \dots + \theta_q \varepsilon_{t-q} + \delta I_t + \varepsilon_t$

Where:

is the intervention variable at time
- $I_t = 1$ starting from the intervention time represents a permanent change.
- $I_t = 1$ only at the time of intervention represents a temporary change (pulse effect).
$\delta$ is the coefficient measuring the impact of the intervention.

There are many other formulations of interventions we can model if we believe that the constant and pulse effects are too simple.

Once we have extended the model with the intervention variable, we can begin the analysis of the intervention’s immediate impact, its duration, and any permanent changes to the level or trend of the series.

The Pros and Cons of Time-Series Modeling

Time-series models are great because they allow us to measure temporal aspects of data. They can account for underlying trends, seasonal effects, and autocorrelation. These are things that are difficult to include in standard regression models. They also allow us to be very explicit in our modeling efforts, making isolating intervention effects from other factors possible.

Time-series models are prone to capturing all variance in a dataset, making isolating interventions difficult. For example, in e-commerce, we see increased spend around the holidays, which correlates with increased revenue from the holiday season. Time-series models may overattribute that cyclical information to seasonality. Selecting a suitable time-series model and specifying the correct form and timing of interventions can also be complex and require sophisticated analytical skills.

Structural Equation Modeling (SEM)

SEM is a comprehensive statistical approach that analyzes complex relationships among observed and unobserved variables. It combines aspects of factor analysis and multiple regression analysis, allowing for the estimation of numerous and interrelated dependence relationships. Specifying a SEM is similar to my post here and Figure 1.

A key strength of SEMs is their ability to handle latent variables. Since we’re discussing halo effects (something that is unobserved), it makes sense to use SEMs.

SEMs are not seen as frequently in the research as other methods. However, they may be employed when we do not have access to consistent time series data. For reference, Burçin & Eren-Erdoğmuş (2016) use an SEM to measure brand loyalty in the hospitality industry.

Since halo effects are unobserved, we can model them as latent variables. A key concept in SEMs is the utilization of indicator variables. Indicator variables are variables we can access that will help estimate our latent variable (halo effect) when combined. Each indicator captures a specific facet of the latent variable. For example, questions in a survey designed to measure “customer satisfaction” might include items about service quality, product performance, and value for money, each serving as a proxy for the broader construct of satisfaction.

To analyze our halo effects, we must first define the effect as a latent variable representing the indirect influence of ToFu marketing spend on BoFu marketing revenue. To do this, we must identify BoFu metrics that ToFu activities could influence. For example, our indicators could be:

Conversion Rate Improvement: An increase in the percentage of leads converting to customers in the BoFu stage.
Increased Customer Lifetime Value: Higher customer value over time indicates long-term engagement and retention.
Upsell/Cross-Sell Rate: Higher rates of existing customers purchasing additional or premium products.

Figure 2. Graph Representing Indicator Variables Within a SEM Model

With our indicators defined, we can now model each BoFu metric as an indicator of the latent halo effect variable. For example, for the conversion rate indicator $C$ , the equation could be:

$C = \lambda_c \times HaloEffect + \epsilon_c$

Where:

$\lambda_c$ is the factor loading for the conversion rate on the halo effect.
$\epsilon_c$ is the error term for the conversion rate.

As you can see, SEMs are powerful and valuable when measuring unobserved metrics in marketing. These frameworks can theoretically measure brand loyalty, awareness, and word-of-mouth. Their flexibility allows SEMs to capture and model these often complex and unobservable relationships, allowing the analyst to understand the marketing mix’s dynamics deeply.

The Pros and Cons of SEMs

SEMs are no free lunch and can become problematic, especially with many variables and paths. The more variables and paths we include, the more data we require, and the more challenging the SEM is to specify and interpret. Another big issue with SEMs is that they are estimated using methods that expect linear relationships. Finally, and importantly, SEMs are not for time-series data by default.

We can overcome some of the issues with SEMs through extensions that exist. By leveraging prior knowledge and probabilistic estimation, Bayesian SEMs accommodate complex models with numerous variables and paths. Additionally, Generalized SEM (GSEM) allows for modeling non-linear relationships and categorical outcomes, providing a more nuanced understanding of marketing dynamics. Using Latent Growth Curve models can also overcome the SEM issue of ignoring the impact of time. By adopting these extensions, analysts can enhance the flexibility and applicability of SEMs in measuring marketing activity, including halo effects.

Technique Selection Guide

Selecting the appropriate analytical technique to measure halo effects requires careful consideration of various factors, including the nature of the data, the specific marketing questions at hand, the complexity of the marketing interactions, and the resources available. Consider starting with simpler models and gradually increasing complexity as needed, ensuring that each step is justified by the data and the theoretical context.

Here’s a guide to help analysts choose the right approach.

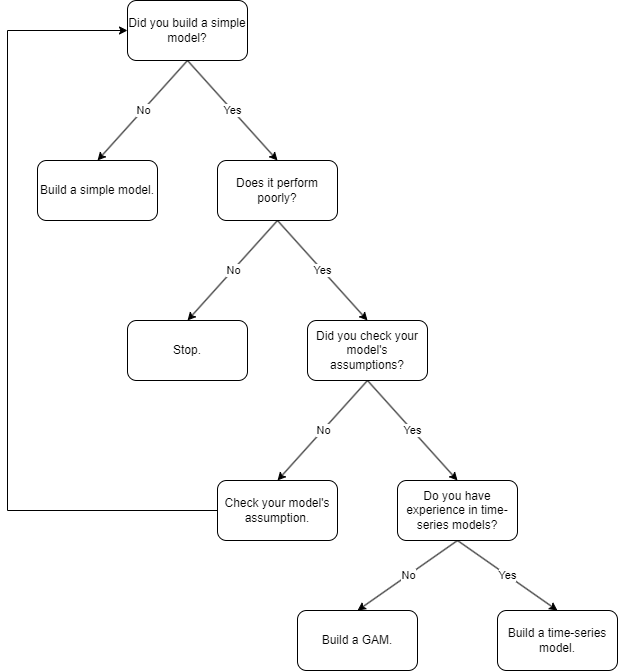
Figure 2. Technique Selection Flow Chart

Selecting the appropriate technique has just as much to do with your skill set as it does with the business problem. I always recommend building a simple model; in this case, time-lagged models are a great start. From there, we can assess the model quality and choose to use more advanced methodologies if necessary.

I do not recommend using time-series models unless you have extensive experience in that domain, as they have much more complicated assumptions than other models. If you are analyzing temporal data, I do not suggest using SEMs as they are difficult to adjust for time-series problems, and we typically consider halo effects in a temporal context.

Conclusion

Measuring halo effects is a crucial step in measuring marketing effects. We see a lot of cannibalization of top-of-funnel efforts by the bottom-of-the-funnel. When disentangling this effect, choosing the correct analytical technique for measuring halo effects is critical.

Carefully assessing your research objectives, data characteristics, and practical constraints and aligning those with the specific needs of your analysis and the nuances of your marketing data will allow you to gain meaningful insights into the complex interplay of marketing activities and their impact on consumer behavior and revenue.

Citations:

Naik, Prasad A., and Kay Peters. “A hierarchical marketing communications model of online and offline media synergies.” Journal of Interactive Marketing 23.4 (2009): 288-299.
Bruce, Norris I., Kay Peters, and Prasad A. Naik. “Discovering how advertising grows sales and builds brands.” Journal of marketing Research 49.6 (2012): 793-806.
Dinner, Isaac M., Harald J. Heerde Van, and Scott A. Neslin. “Driving online and offline sales: The cross-channel effects of traditional, online display, and paid search advertising.” Journal of marketing research 51.5 (2014): 527-545.
Dekimpe, M. G., & Hanssens, D. M. (2004). Persistence modeling for assessing marketing strategy performance. Available at SSRN 474428.
Leone, Robert P. “Modeling Sales-Advertising Relationships: An Integrated Time Series–Econometric Approach.” Journal of Marketing Research 20.3 (1983): 291-295.
Tatar, Şahika Burçin, and İrem Eren-Erdoğmuş. “The effect of social media marketing on brand trust and brand loyalty for hotels.” Information Technology & Tourism 16 (2016): 249-263.